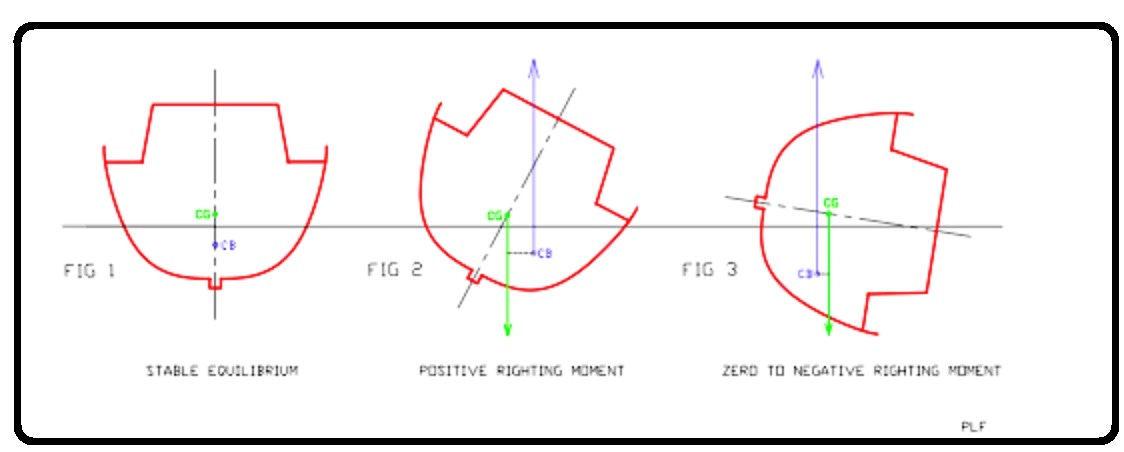
Why Yachts Don't Just Turn Upside Down

A BRIEF PRIMER ON STABILITY

Preface: When it comes to discussing stability in yachts and other vessels, nearly impenetrable jargon is often resorted to — terms like “metacentric height”, “GM”, “inclining”, “roll period”. And when the explanation is over, you can see by the glaze in the eyes of the reader or listener that the product of the explanation does not include insight or u…